Examination Questions in Quadrilaterals

Click on the option you think is right and then check by clicking on the Show Answer button. You can change your option as many times as you like.

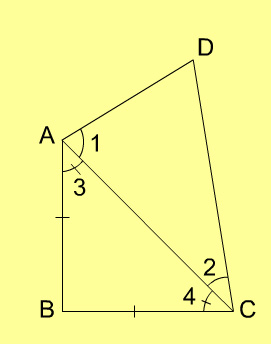
1. ABCD is a quadrilateral such that BC = BA and CD > AD. Which one of the following is correct?  

  1. angle BAD = angle BCD
  2. angle BAD < angle BCD
  3. angle BAD > angle BCD
  4. 2angle BAD = angle BCD

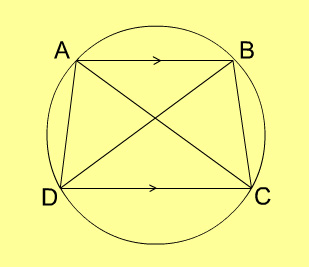
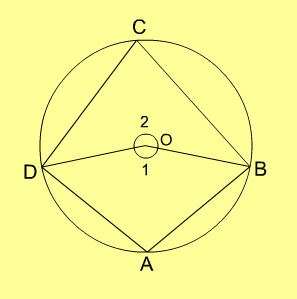
2. A quadrilateral ABCD is inscribed in a circle. If AB is parallel to CD but AD is not parallel to BC and AC = BD, then the quadrilateral must be a  

  1. parallelogram
  2. rhombus
  3. trapezium
  4. None of the above

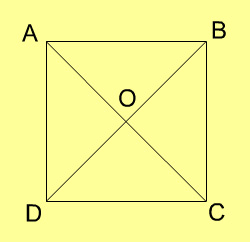
3. If the diagonals of a quadrilateral are equal and bisect each other at right angles, then the quadrilateral is a  

  1. rectangle
  2. square
  3. rhombus
  4. trapezium

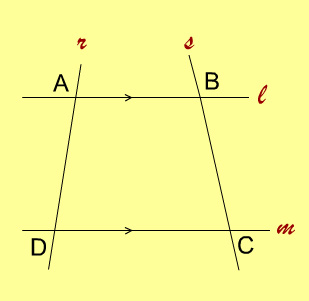
4. If two parallel lines are cut by two distinct transversals, then the quadrilateral formed by the four lines is always a  

  1. square
  2. parallelogram
  3. rhombus
  4. trapezium

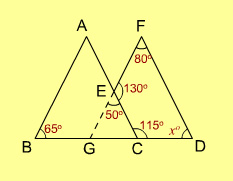
5. answerimage5

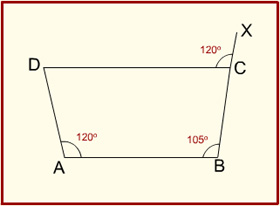
In the quadrilateral ABCD shown above, ∠DAB = ∠DCX = 120°. If ∠ABC = 105°, what is ∠ADC equal to?  

  1. 45°
  2. 60°
  3. 75°
  4. 95°

6. If A, B, C, D are the successive angles of cyclic quadrilateral, then what is cos A + cos B + cos C + cos D equal to?  

  1. 4
  2. 2
  3. 1
  4. 0

7. Consider the following statements:

  1. The opposite angles of a cyclic quadrilateral are supplementary.
  2. Angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.

Which one of the following is correct in respect of the above statements?  

  1. Statement-1 => statement-2
  2. Statement-2 => statement-1
  3. Statement-1 => statement-2
  4. Neither statement-1 => statement-2 nor statement-2 = statement-1

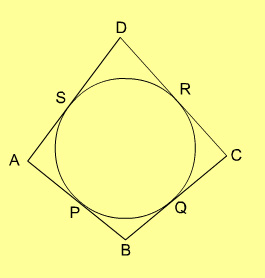
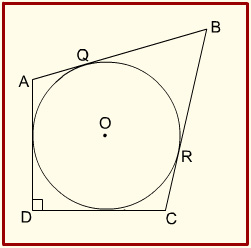
8. ABCD is a quadrilateral, the sides of which touch a circle. Which one of the following is correct?  

  1. AB + AD = CB + CD
  2. AB : CD = AD : BC
  3. AB + CD = AD + BC
  4. AB : AD = CB : CD

9. answerimage9

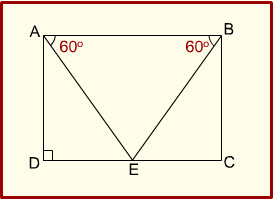
In the figure given, ABCD is a quadrilateral with AB parallel to DC and AD parallel to BC. ADC is a right angle. If the perimeter of the triangle ABE is 6 units, what is the area of the quadrilateral?  

  1. 2√3 square units
  2. 4 square units
  3. 3 square units
  4. 4√3 square units