PRACTICE QUESTIONS ON CIRCLES

Examination Questions on Circles

Click on the Show Answer button to see the answer.

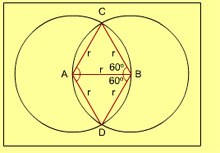
1. Each of the two circles of equal radii with centres at A and B pass through the centre of one another. If they cut at C and D then angle DBC is equal to :  

1. 60°
2. 100°
3. 120°
4. 140°

Answer (c). Triangles ACB and DBA are equilateral triangles because they have radius r as their sides. Thus angles CBA and ABD are each equal to 60 degrees making angle DBC equal to 120 degrees.

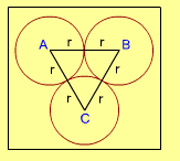
2. The three equal circles touch each other externally. If the centres of these circles be A, B, C then triangle ABC is :  

1. a right angle triangle
2. an equilateral triangle
3. an isosceles triangle
4. a scalene triangle

Answer (b). Each side of the triangle is equal to twice the radius of a circle.

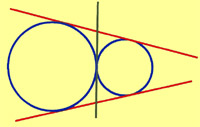
3. The minimum numbers of common tangents drawn to two circles when both the circle touch externally is :  

1. 0
2. 1
3. 2
4. 3

Answer (d).

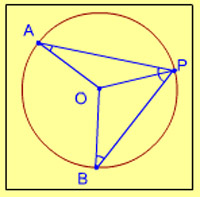
4. A, B, P are three points on a circle having centre O. If angle OAP = 25° and angle OBP = 35°, then the measure of angle AOB is  

1. 120°
2. 60°
3. 75°
4. 150°

Answer (a). Since OA, OB, OP are each equal to radius of the circle, triangles OAP and OBP are isosceles triangles. Thus angle OAP = OPA = 25^o and angle OBP = OPB = 35^o and angle BOP = 110^o and angle AOP = 130^o. Therefore angle AOB = 360^o - 240^o = 120^o.
Shortcut: Angle subtended at the centre of a circle by an arc (in this case arc AB) is double the angle subtended by it on any point on the remaining part of the circle. Since angle subtended at any other point P is 25^o + 35^o = 60^o, the angle subtended at the centre is 120^o.

5. ABCD is a cyclic quadrilateral, AB is a diameter of the circle. If angle ACD = 50° , the value of angle BAD is  

1. 30°
2. 40°
3. 50°
4. 60°

Answer (b).
Angle ACB=90^o (angle subtended by the diameter of a circle) and angle ACD =50^o (given).
Angle DCB = 90^o + 50^o = 140^o
Therefore, angle BAD = 180^o - 140^o = 40^o
Property: The sum of opposite angles of a cyclic quadrilateral is 180^o.

6. Two circles of equal radii touch externally at a point P. From a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and R respectively. The relation of TQ and TR is  

1. TQ < TR
2. TQ > TR
3. TQ = 2 TR
4. TQ = TR

Answer (d). From the figure congruence of 2 quadrilaterals PBQT and PART can be proven.

7. AB is the chord of a circle with centre O and DOC is a line segment originating from a point D on the circle and intersecting AB produced at C such that BC = OD. If angle BCD = 20° , then angle AOD = ?  

1. 20°
2. 30°
3. 40°
4. 60°

Answer (d).
Triangle OBC and OBA are both isosceles triangles.
In triangle OBC, angle OBC = 180^o - (20^o + 20^o) = 140^o.
In triangle OBA, angle OBA = 180^o - 140^o = 40^o.
Angle OAB = 180^o - (40^o + 40^o) = 100^o.
Therefore Angle OAD = 180^o - (100^o + 20^o) = 60^o.

8. In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. If both the chords are on the same side of the centre, then the distance between the chords is  

1. 9 cm
2. 7 cm
3. 23 cm
4. 11 cm

Answer (b).
In triangle OED, OD = 17 cm and ED = 16/2 = 8 cm.
Applying Pythagoras, OE = 15 cm
In triangle OFB, OB = 17 cm and FB = 30/2 = 15 cm
Applying Pythagoras, OF = 8 cm.
Thus the distance between the two chords EF = 15 - 8 = 7 cm.

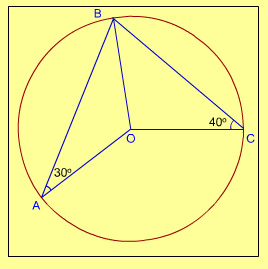
9. O is the centre of the circle passing through the points A, B and C such that angle BAO = 30^o, angle BCO = 40^o and angle AOC = x^o. What is the value of x?  

1. 70^o
2. 140^o
3. 210^o
4. 280^o

Answer (b). Triangles BOC and AOC are both isosceles triangles since OA, OB and OC are equal to the radius of the circle.
Therefore, angle OBC = 40^o and angle OBA = 30^o.
==> angle AOB = 180^o - (2 x 30^o) = 120^o
==> angle BOC = 180^o - (2 x 40^o) = 100^o.
Hence angle AOC = 360^o - (120^o + 100^o) = 140^o.

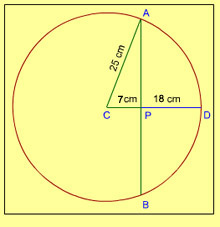
10. The diameter of a circle with centre at C is 50 cm. CP is a radial segment of the circle. AB is a chord perpendicular to CP and passes through P. CP produced intersects the circle at D. If DP = 18 cm, then what is the length of AB?  

1. 24 cm
2. 32 cm
3. 40 cm
4. 48 cm

Answer (d). In the triangle APC, AP² = CA² - CP²
==> AP = 625 – 49 = √576 = 24 cm
Similarly, PB = 24 cm
Therefore AB = AP + PB = 48 cm.

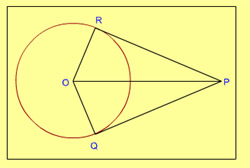
11. From a point P which is at a distance of 13 cm from centre O of a circle of radius 5 cm, in the same plane, a pair of tangents PQ and PR are drawn to the circle. Area of quadrilateral PQOR is  

1. 65 sq cm
2. 60 sq cm
3. 30 sq cm
4. 90 sq cm

Answer (b). OP = 13 cm and OR = OQ = 5 cm ....given
Angle ORP and OQP = 90^o ...radius is perpendicular to a tangent at the point of incidence.
Applying Pythagoras PR and PQ = 12 cm.
Area of each triangle = (5 x 12)/2 = 30 sq cm.
Thus area of quadrilateral = 60 sq cm.

12. The diameters of two circles are the side of a square and the diagonal of the square. The ratio of the areas of the smaller circle and the larger circle is  

1. √2 : √3
2. 1 : √2
3. 1 : 2
4. 1 : 4

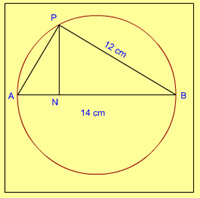
13. N is the foot of t\he perpendicular from a point P of a circle with radius 7 cm, on a diameter AB of the circle. If the length of the chord PB is 12 cm, the distance of the point N from the point B is  

1. 3 ⁵/₇ cm
2. 10 ²/₇ cm
3. 6 ⁵/₇ cm
4. 12 ²/₇ cm

Answer (b). In the right triangle APB, AP can be found out using Pythagoras which comes to √52.
In triangle PNB, PN² = PB² - NB²
= PB² - (14 - AN)² .....1
In triangle ANP, PN² = AP² - AN ² .....2
Equating (1) and (2), PB² - (14 - AN)² = AP² - AN ²
144 - 196 - AN² + 28AN = (√52)² - AN²
AN = 3 ⁵/₇
NB = 14 - 3 ⁵/₇ = 10 ²/₇

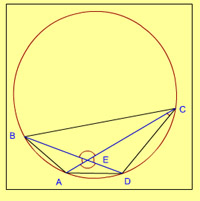
14. A,B.C,D are four points on a circle,AC and BD intersect at a point E such that angle BEC=130° and ECD=20°.Angle BAC is  

1. 100°
2. 110°
3. 120°
4. 90°

Answer (b). In triangle ECD,
angle ECD = 20^o
angle CED = 50^o (180^o - 130^o = 50^o)
Therefore angle EDC = 110^o.
Angle BAC is also = 110^o (since angles subtended in the same segment are equal.)

15. The radius of a circle is a side of a square. The ratio of the areas of the circle and the square is  

1. π : 2
2. 2 : π
3. 1 : π
4. π : 1

16. A cow is tied by a rope to a post at the centre of a field. If it stretches the rope fully and describes an arc of length 44 metres while tracing an angle of 36^o, what is the length of the rope? (Take pi = 22/7)

1. 66 metres
2. 68 metres
3. 70 metres
4. 72 metres

• <–– Trains
• Triangles ––>

Geometry

Others

Arithmetic