PRACTICE QUESTIONS ON TRIANGLES
TERMINOLOGY RELATED TO TRIANGLES
- Median – A line segment from a vertex to the midpoint of the opposite side.
- Centroid – The point where all three medians of a triangle intersect.
- Orthocenter – The point where all three altitudes intersect.
- Circumcenter – The point where all three perpendicular bisectors intersect; the center of the triangle’s circumcircle.
- Incenter – The point where all three angle bisectors meet; the center of the incircle.
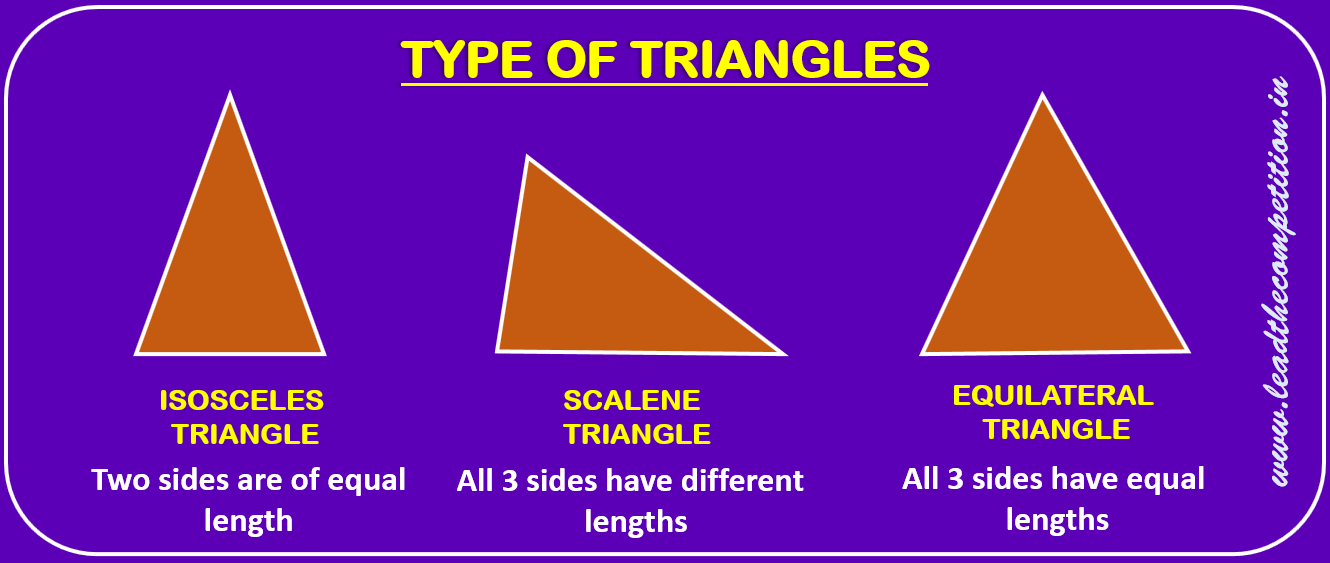
TYPES OF TRIANGLES
The figure below shows the different types of triangles based on the length of their sides. An isosceles triangle is one in which 2 sides are equal in length. An equilaterial triangle is one in which all the three sides are equal in length, while a scalene triangle is one in which all the three sides are of different lengths.
Simple Quiz on Triangles
Examination Questions on Triangles
Click on the option you think is right and then check by clicking on the Show Answer button. You can change your option as many times as you like.
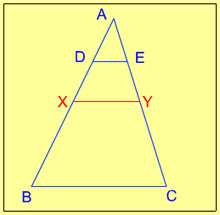
1. For a triangle ABC, D and E are two points on AB and AC such that AD = 1/4AB, AE = 1/4AC. If BC = 12 cm then DE is :
- 3 cm
- 6 cm
- 5 cm
- 4 cm
2. In an acute angled triangle ABC, if sin 2(A + B – C)= 1 and tan(B + C – A) = √3, then the value of angle B is
- 60°
- 30°
- 52 ½°
- 67 ½°
3. If the in radius of a triangle with perimeter 32 cm is 6 cm, then the area of the triangle in sq. cm is
- 48
- 100
- 64
- 96
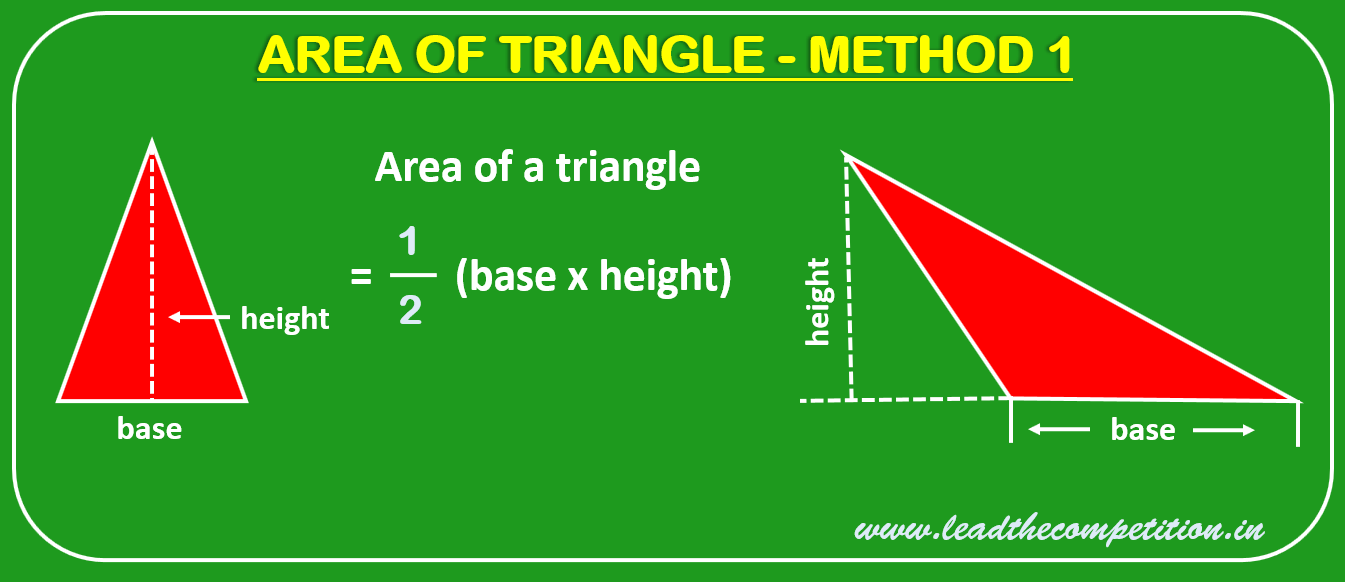
Calculation of Area of a Triangle
There are several ways in which the area of a triangle can be calculated depending on the information available. The most common method is dividing the product of the length of its base and height by 2. The figure below depicts the use of the identity for calculation of area of a triangle.
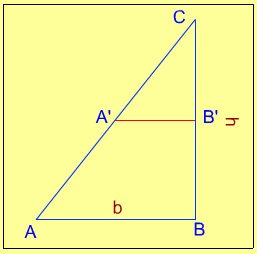
4. ABC is a right angled triangle, B being the right angle. Mid-points of BC and AC are respectively B’ and A’. The ratio of the area of the quadrilateral AA’ B’B to the area of the triangle ABC is
- 1 : 2
- 2 : 3
- 3 : 4
- None of the above
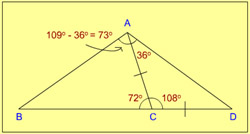
5. In a triangle ABC, the side BC is extended up to D. Such that CD = AC, if angle BAD = 109° and angle ACB = 72° then the value of angle ABC is
- 35°
- 60°
- 40°
- 45°
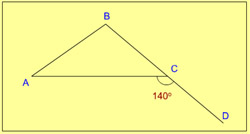
6. Side BC of triangle ABC is produced to D. If angle ACD = 140o and angle ABC = 3 ⁄BAC, then find angle A.
- 45°
- 55°
- 35°
- 60°
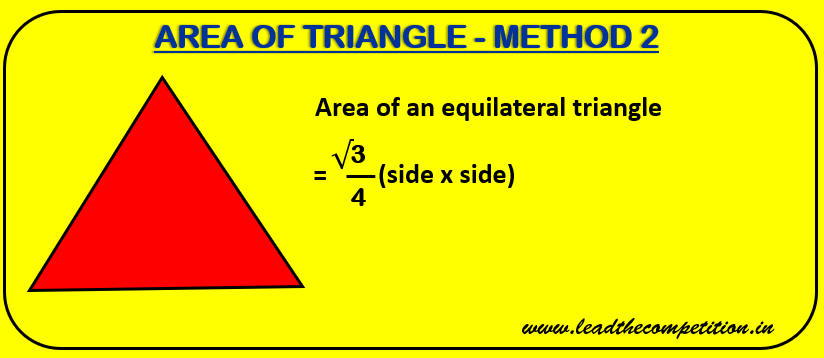
Calculation of Area of an Equilateral Triangle
An equilateral triangle is a unique figure which has equal sides and 3 equal angles and it has a unique formula for calculation of its area based on the length of its side.
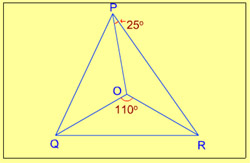
7. If O be the circum centre of a triangle PQR and angle QOR = 110°, angle OPR = 25°, then the measure of angle PRQ is
- 55°
- 60°
- 65°
- 50°
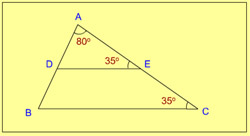
8. D and E are mid-points of AB and AC of triangle ABC. If angle A = 80o, angle C = 35o, then angle EDB is equal to
- 100°
- 115°
- 120°
- 125°
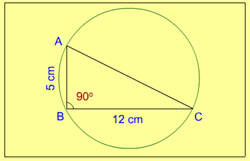
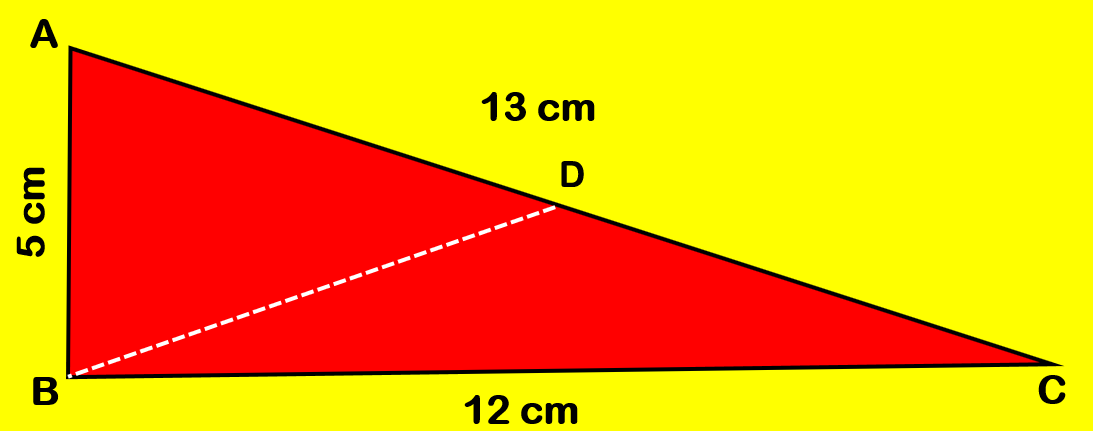
9. In a right-angled triangle ABC, angle ABC = 90°, AB = 5 cm and BC = 12 cm. The radius of the circum circle of the triangle ABC is
- 6.5 cm
- 7 cm
- 7.5 cm
- 6 cm
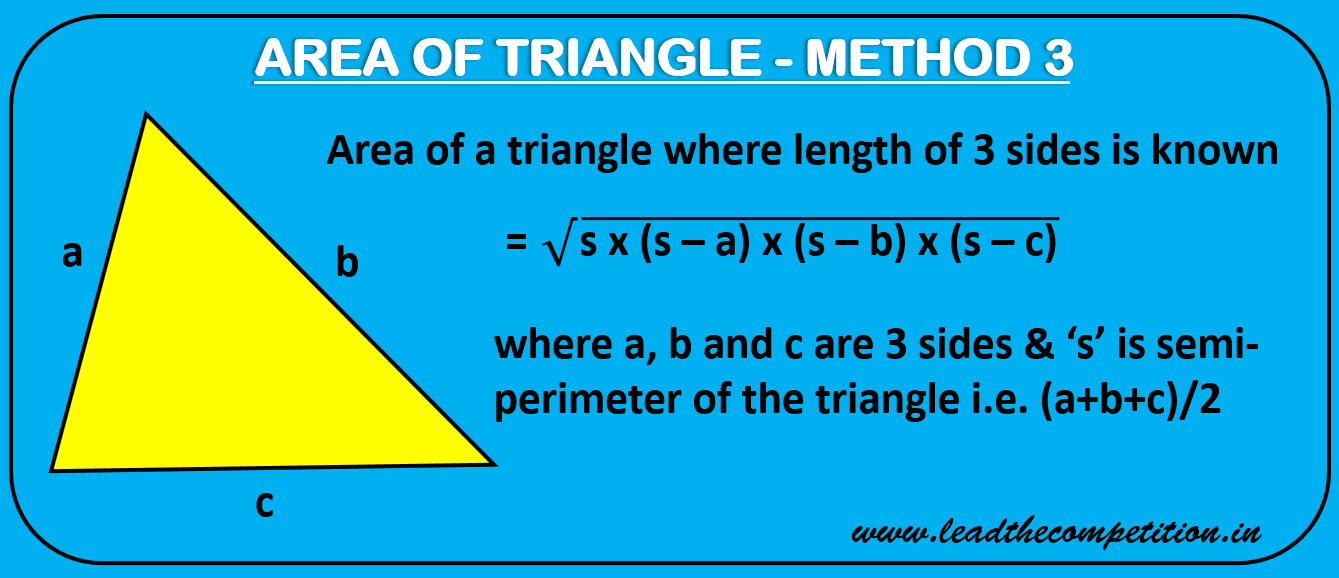
Heron's Formula
Calculation of area of a triangle where the length of its 3 sides is known: Area of any triangle can also be calculated if the lenght of its three sides is known. This is known as Heron's formula.
10. If the circum radius of an equilateral triangle ABC be 8 cm, then the height of the triangle is
- 8 cm
- 12 cm
- 16 cm
- 6 cm
11. 360 sq. cm and 250 sq. cm are the areas of two similar triangles. If the length of one of the sides of the first triangle be 8 cm, then the length of the correspoding side of the second triangle is
- 6 cm
- 6 1/5 cm
- 6 1/3 cm
- 6 2/3 cm
12. If the perimeters of an equilateral triangle and that of a square are equal, then the ratio of their areas will be
- 4 : 3
- 4 : √3
- 4 : 3√3
- 4 : 2√3
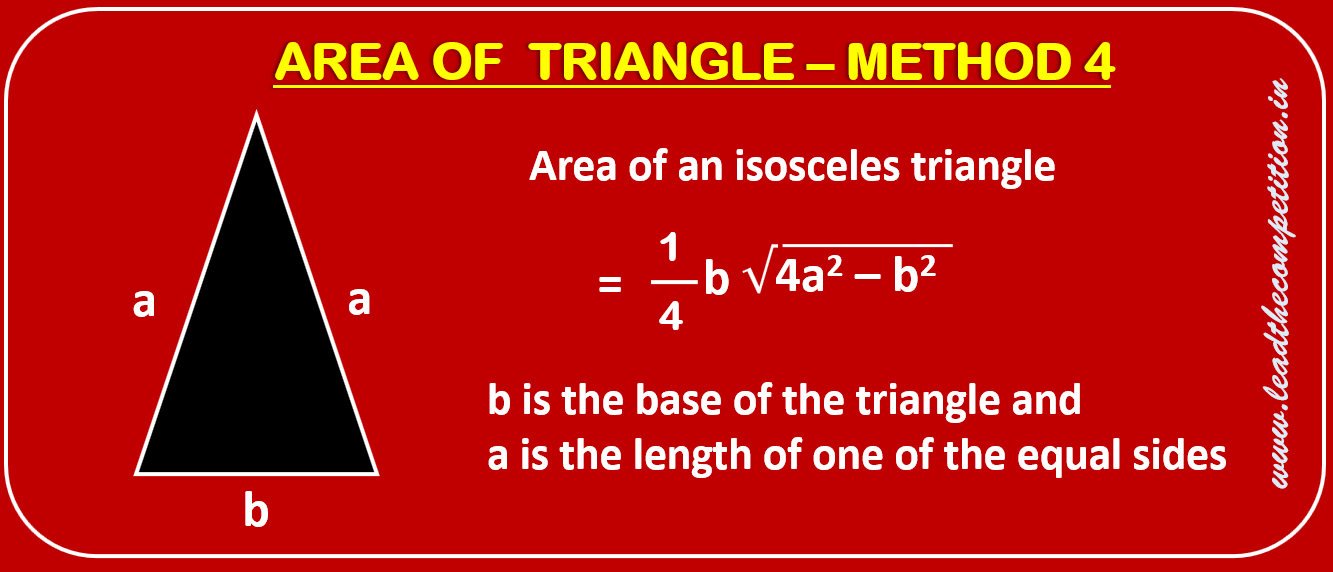
Calculation of Area of an Isosceles Triangle
Just like an equilateral triangle, an isosceles triangle also has a unique a unique formula for calculation of its area based on the length of its equal side and the length of its base.
13. Length of each equal side of an isosceles triangle is 10 cm and the included angle between those two sides is 45o. Find the area of the triangle.
- 25√2 cm2
- 35√2 cm2
- 5√2 cm2
- 15√2 cm2
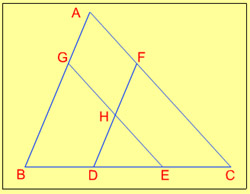
14. In a triangle ABC, the base BC is trisected at D and E. The line through D, parallel to AB, meets AC at F and the line through E parallel to AC meets AB at G. Let EG and DF intersect at H. What is the ratio of the sum of the area of parallelogram AGHF and the area of the triangle DHE to the area of the triangle ABC?
- 1 : 2
- 1 : 3
- 1 : 4
- 1 : 6
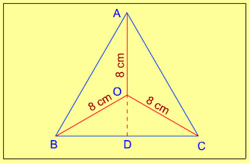
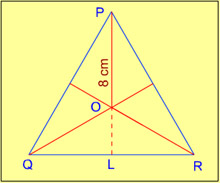
15. PQR is an equilateral triangle. O is the point of intersection of altitudes PL, QM and RN. If OP = 8 cm, then what is the perimeter of the triangle PQR?
- 8√3 cm
- 12√3 cm
- 16√3 cm
- 24√3 cm
16. ABC is a triangle. The bisectors of the internal angle B and external angle C intersect at D. If angle BDC = 50o, then angle A is
- 100o
- 90o
- 120o
- 60o
Properties of triangle: Like all geometric figures, a triangle too has certain unique properties. Listed below are some of them.

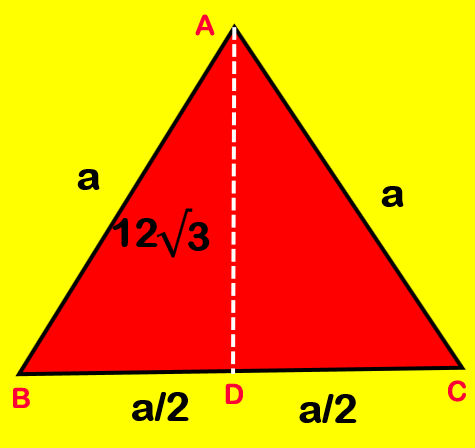
17. If the altitude of an equilateral triangle is 12√3 cm, then its area would be:
- 12 cm2
- 72 cm2
- 36√3 cm2
- 144√3 cm2
18. If the area of an equilateral triangle is 9√3 sq cm, then what would be its altitude?
- 6 cm
- 6√3 cm
- 3√3 cm
- 9√3 cm

19. What is the ratio of areas of two similar triangles if the sides are in the ratio 5:7?
- 5 : 7
- 10 : 14
- 25 : 49
- 125 : 343
20. A triangle has 3 sides of length 5 cm, 12 cm and 13 cm. What would be the length of the median from the hypotenuse to its opposite vertex?
- 6.5 cm
- 6 cm
- 7 cm
- 5.5 cm